Continuously Indexed Domain Adaptation

Hao Wang*, Hao He*, Dina Katabi.
Massachusetts Institute of Technology

This blog post brief introduces key points of CIDA. The full paper can be downloaded here.

Overview

Domain adaptation (DA) transfers knowledge from domain A to domain B. Can we go beyond this categorical treatment and adapt across infinite domains indexed by a continuous number? In our ICML 2020 paper ”Continuously Indexed Domain Adaptation”, we make the first attempt to do so and verify our approach both empirically and theoretically.

Fortunately reviewers seem to agree with us and like our work as well: ) Here are AC’s exact words in the meta-review: “This paper addresses the topic of domain adaptation for continuous domains. This work is unanimously considered very novel, of high impact - effective problems in the medical domain, with good theoretical and experimental results presented.”

Outline

Categorical DA versus Continuously Indexed DA

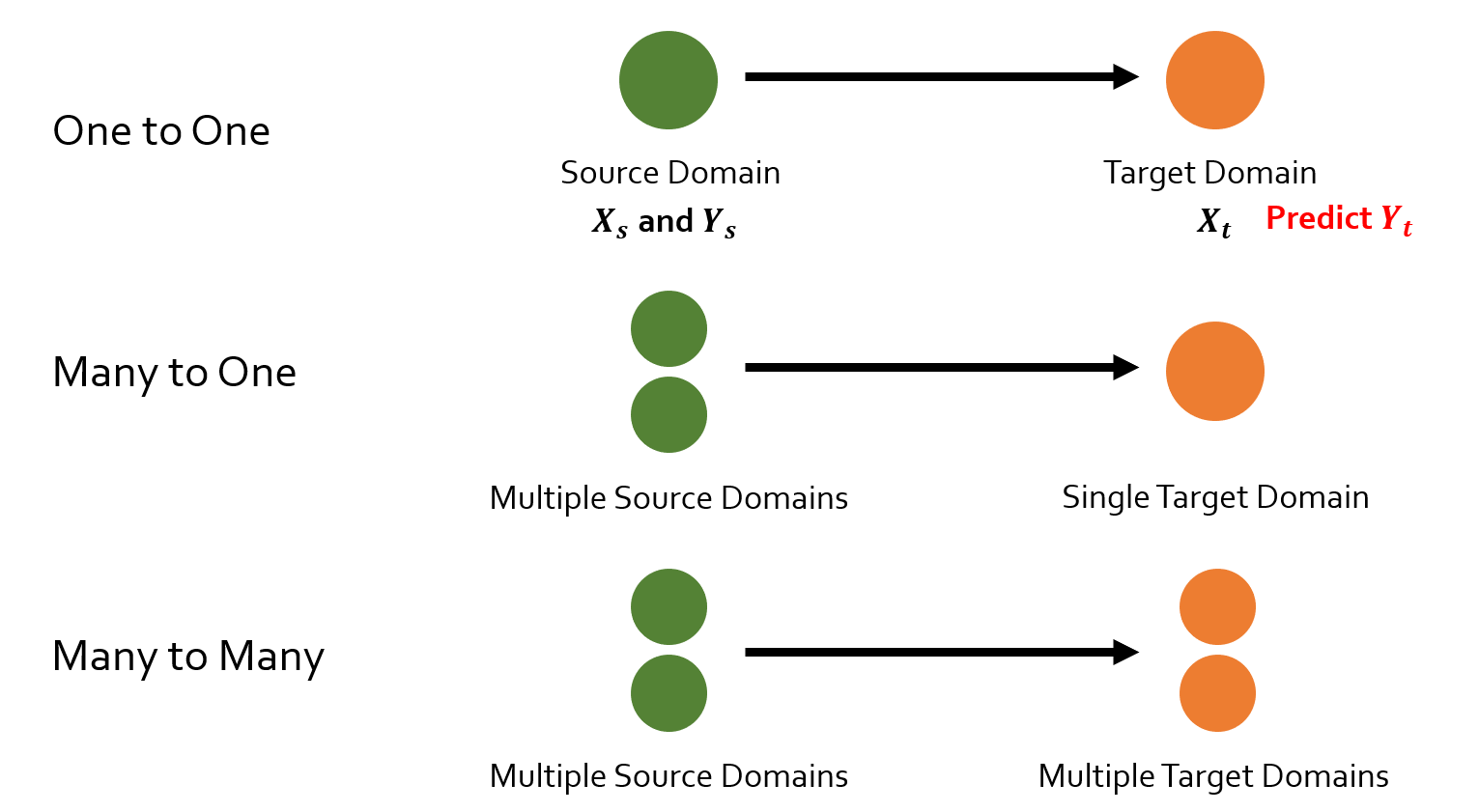
Traditional DA adapts from one (or many) domains to another (few) domains, as shown in the figure below:

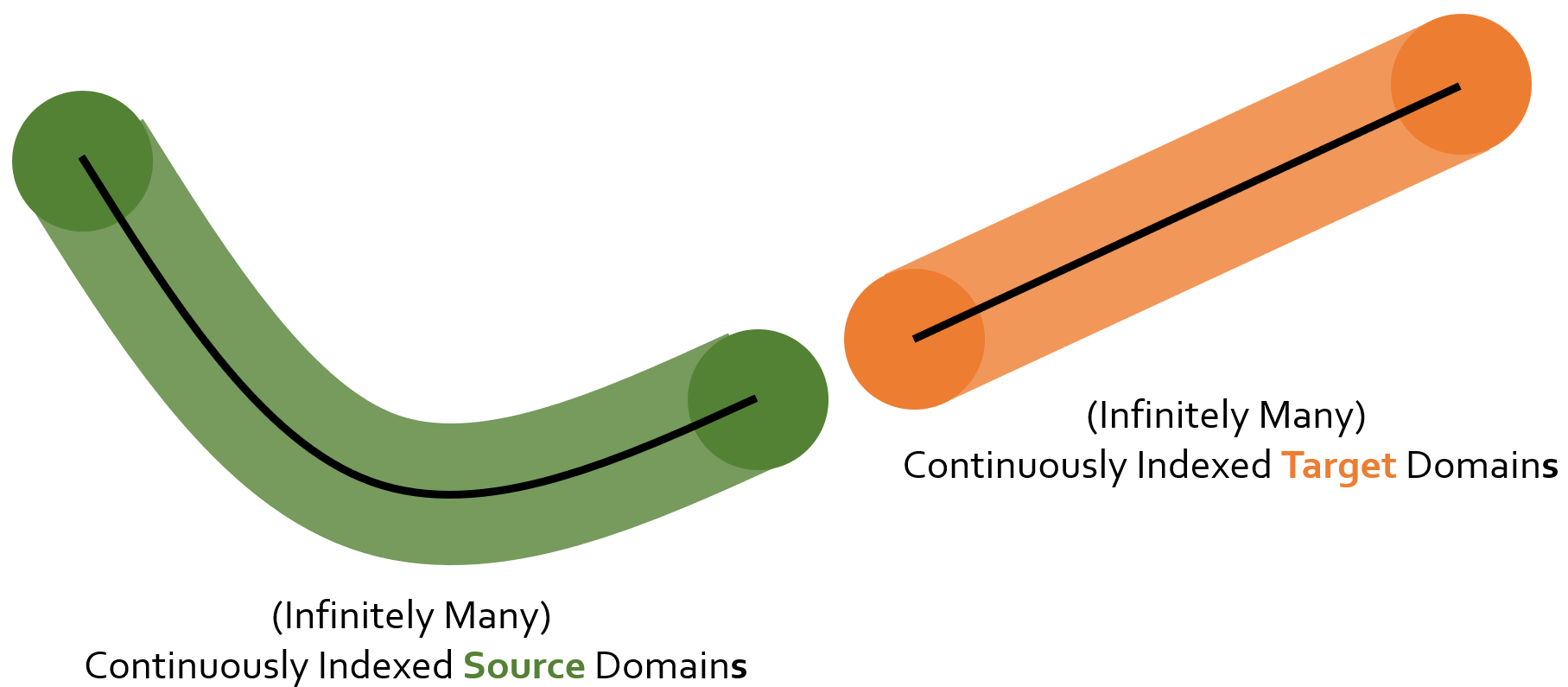
However we find that: in practice, things are often more complicated. Domains are not exist separately; instead they exist in a continuous spectrum. For example, in medical applications (see the figure below), patients of different ages belong to different domains, and ‘age’ is a continuous notion. Therefore, we what need is actually adaptation across infinitely many continuously (indexed) domains.

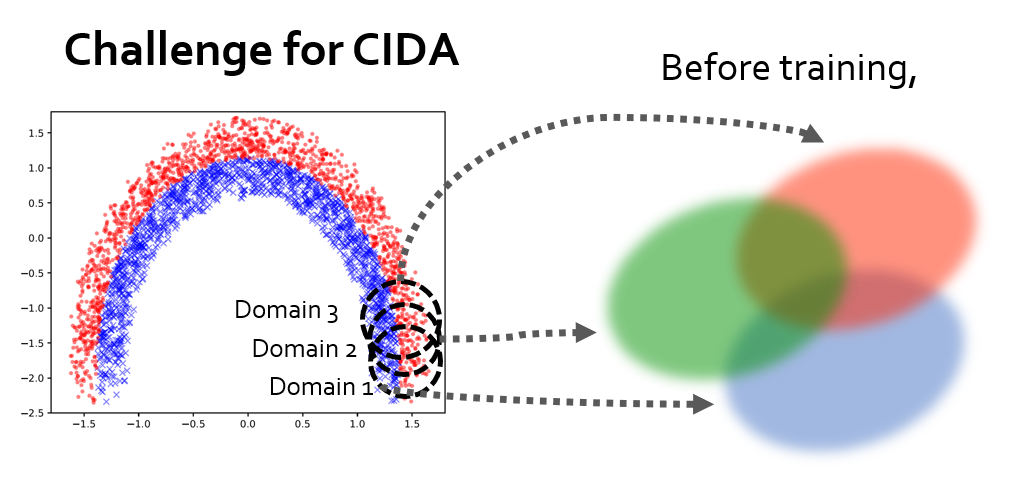
And we call this task we identify ‘continuously indexed domain adaptation’. As shown in the figure below: we can have infinitely many source domains (on the left) and infinitely many target domains (on the right).

Illustrating Example Using a Toy Dataset

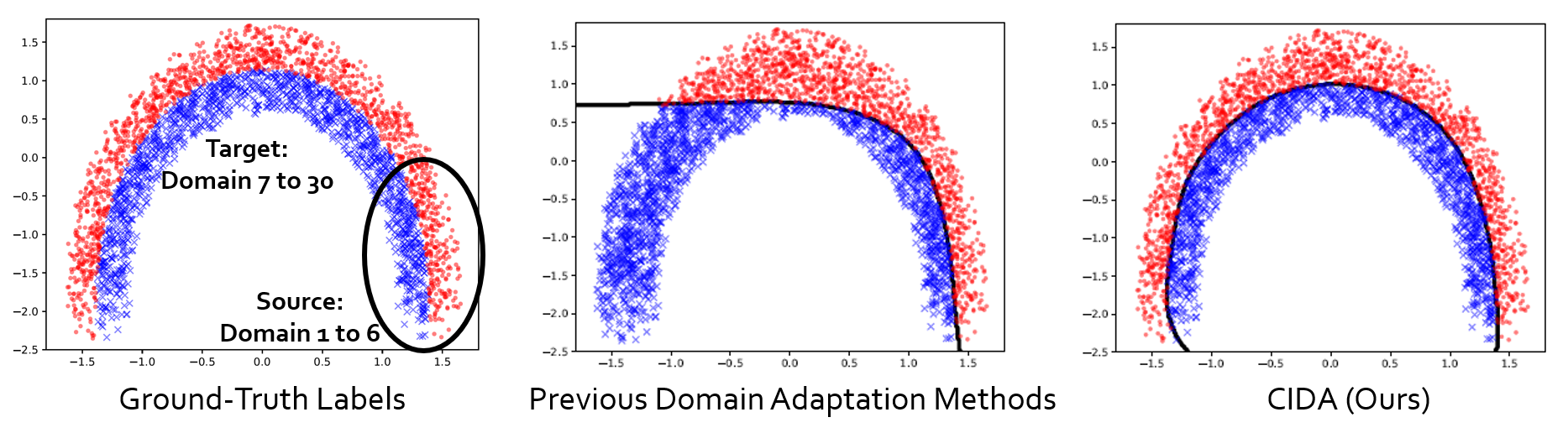
As an illustrating example, take a look at the figure below. Imagine we have 30 domains on the same trajectory, and let’s treat domain [1, 6] as source domains with the rest as target domains. Obviously, traditional categorical DA does not learn the correct decision boundary, while our continuous DA does. Here we name our method Continuously Indexed Domain Adaptation (CIDA, pronounced as ‘cider’).

Method

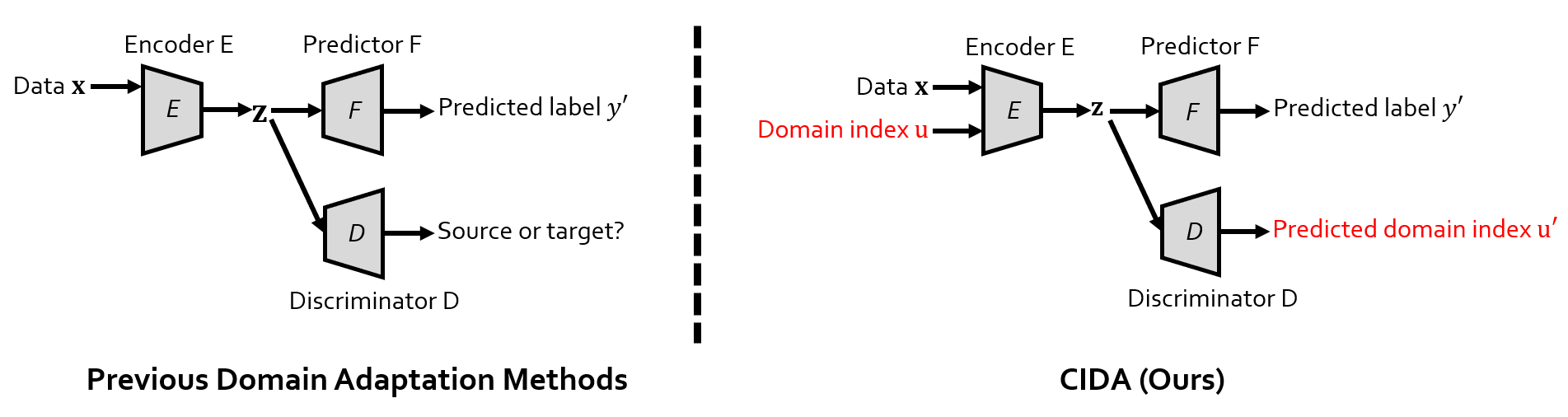
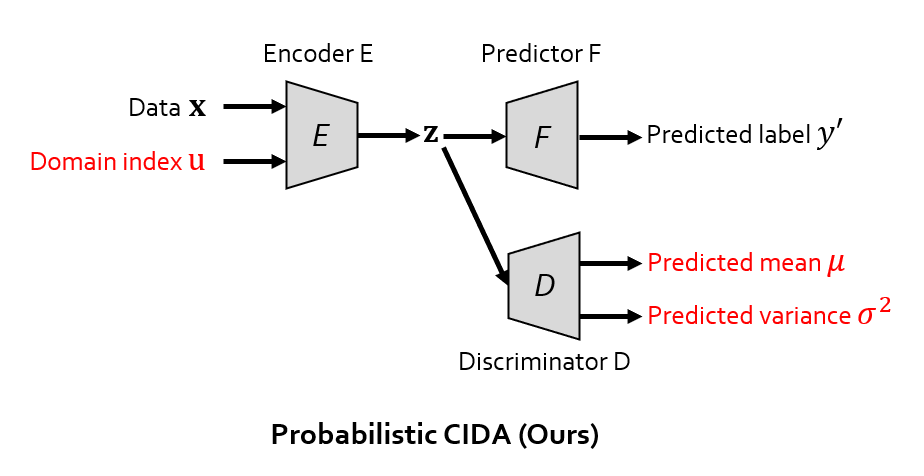
Interestingly, implementing CIDA is quite simple. For those of you who are familiar with adversarial domain adaptation, one glance at the figure below and you will get it: ) The differences between our CIDA and traditional adversarial DA are marked in red.

Here we introduce the concept of ‘domain index’, denoted as u in the figure. For example, u can be the age of patients in medical applications. z is the encoding, i.e., the output of the encoder. The figure below basically means: you only need to feed the domain index u into the encoder, let the discriminator predict (regress) u, and train the whole model adversarially.

However, this is not the end of the story: ) Though CIDA does very well on most cases, theoretically we find that if the discriminator directly predicts the domain index u as a scalar value, the model can only align the mean of p(u | z) for different domains, meaning that only the first moment is matched. This can lead to a not-so-good local optimum. For example, if we look at the first 3 domains in the toy dataset (shown in the figure below),

If we directly use the vanilla CIDA, it may end up with the following worst case. We can see that the 3 domains on the right of the figure are not aligned, but the means of their corresponding p(u | z) are identical.

So, how do we address this problem? We later find that, on the right of the figure above, although the means (expectations) E[u | z] for the 3 domains is identical, their variances V[u | z] are not! This lead us to an advanced version of CIDA, which we call probabilistic CIDA, or PCIDA in short (shown in the figure below). All we need to do is let the discriminator simultaneously predict the mean and the variance, and use the Gaussian log-likelihood as the objective function.

Theory

What’s more interesting is that theoretically we can prove that (see the figure below): when CIDA and PCIDA are trained to their optimal points, it is guaranteed that the mean and variance of p(u | z) are aligned for any domain index u (Theorem 1 and 2 below). What’s more, the addition of discriminators will not harm the predictors’ performance (Theorem 3). In other words, using CIDA is always better than not using it. For full theorems and proofs please refer to the paper.

Experiments on Rotating MNIST

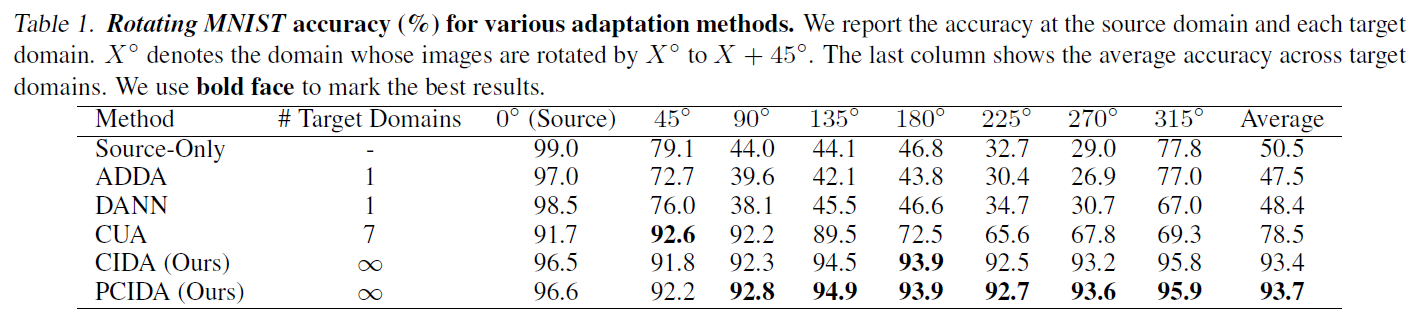
Besides the toy dataset above, we also conduct experiments on a dataset with ‘nearly infinitely many’ domains: Rotating MNIST. This is a dataset we construct based on MNIST. We use rotation angle as the domain index to generate hundreds of thousands of digits, each with a different rotation angle (domain index). See the results below. The column with ‘45’ means digits with angle in the range [45, 90), and the column with ‘90’ means digits with angle in the range [90, 135), etc. We can see that CIDA obviously outperforms all previous DA methods.

Experiments on Real-World Medical Datasets

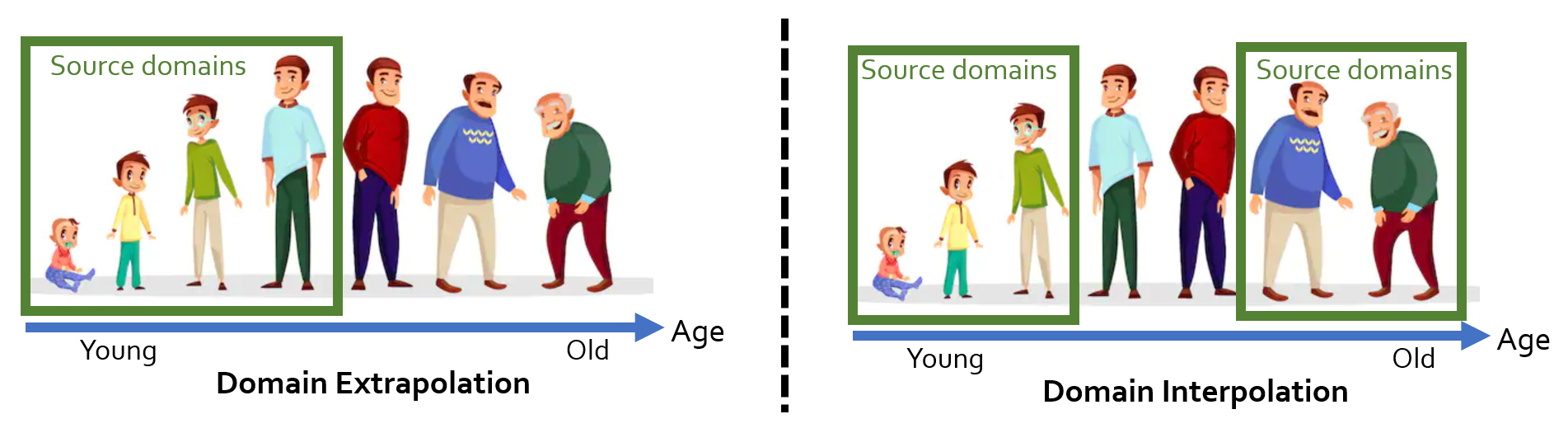
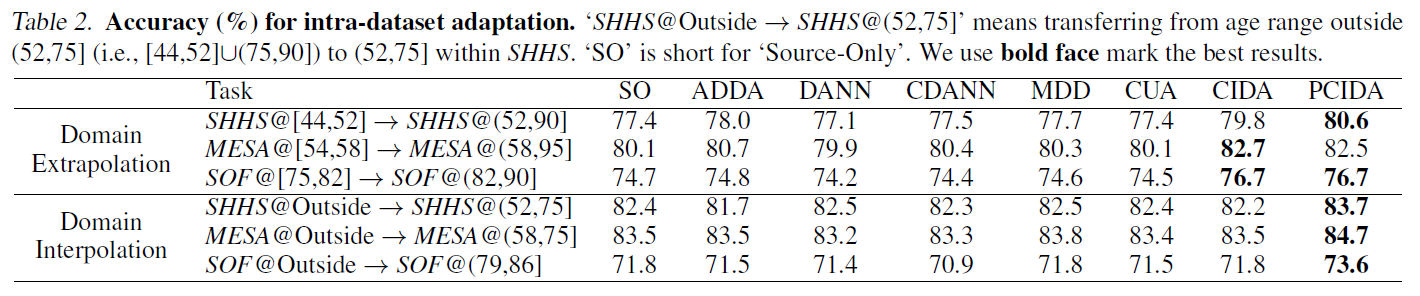
We also verify our methods on several real-world medical datasets. For simplicity, we focus on a classification task with the patients’ age as the domain index. For each dataset, we consider two settings: domain extrapolation and domain interpolation (see the figure below).

The table below shows the results when adapting across patients of different ages.

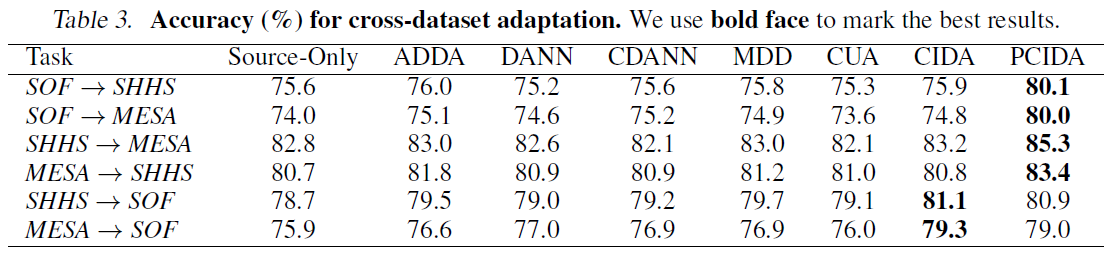
Below are results for the cross-dataset setting.

Three observations: (1) Categorical DA may hurt performance (surprisingly but not surprisingly). (2) CIDA/PCIDA improve performance in both settings. (3) CIDA/PCIDA has larger performance gain in extrapolation since it is harder.

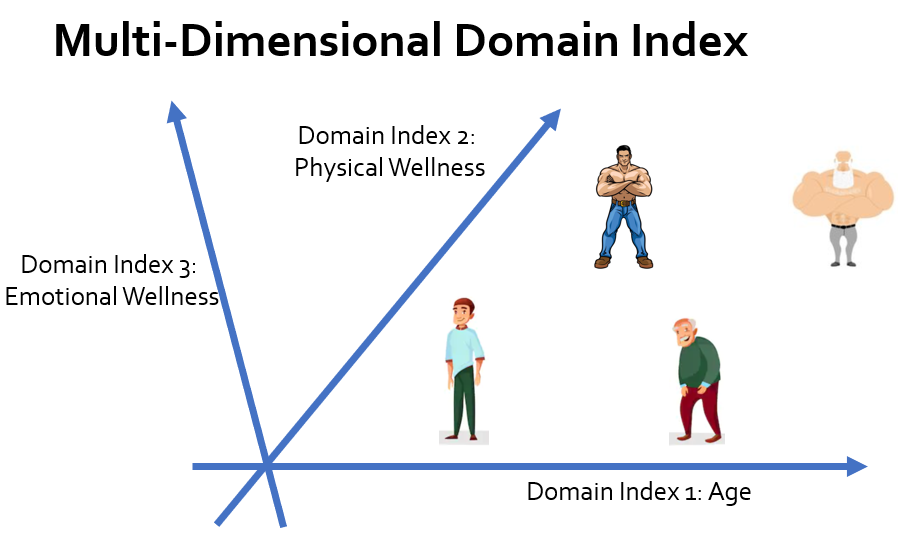
One More Thing: Multi-Dimensional Domain Index

During the development of CIDA, we find that oftentimes there may be multiple (different) domain indices that affects prediction, e.g., age and physical wellness (measured with a score from 0 to 100). We therefore propose this new idea of ‘multi-dimensional domain index’ (see the figure below).

Materials and Reference

Paper: https://arxiv.org/abs/2007.01807 or http://wanghao.in/paper/ICML20_CIDA.pdf 

Video: https://drive.google.com/file/d/1G_51ekjcCTFRsvnGYiR5yFxBItWH2YBp/view

ICML Talk: https://icml.cc/virtual/2020/poster/5986 

Reference:

@inproceedings{DBLP:conf/icml/WangHK20,

  author    = {Hao Wang and

               Hao He and

               Dina Katabi},

  title     = {Continuously Indexed Domain Adaptation},

  booktitle = {ICML},

  year      = {2020}

}

Also Check Out: