A Survey on Bayesian Deep Learning

Hao Wang Dit-Yan Yeung

Massachusetts Institute of Technology

Hong Kong University of Science and Technology

This blog post brief introduces some key points of the survey. The full paper can be downloaded here.

Background

In 2014~2016, we proposed a probabilistic framework called Bayesian deep learning (BDL) to unify modern deep learning and probabilistic graphical models. The past half a decade has witnessed a myriad of methods proposed under the Bayesian deep learning framework. In the meantime, the semantics of Bayesian deep learning have also experienced subtle evolutions. In this survey paper published in ACM Computing Surveys, we thoroughly review and discuss methods under the framework as well as other related topics such as Bayesian neural networks.

BDL Sensu Lato and BDL Sensu Stricto

In the survey, we make a distinction between BDL sensu lato (i.e., BDL in a broader sense) and BDL sensu stricto (i.e., BDL in a narrower sense).

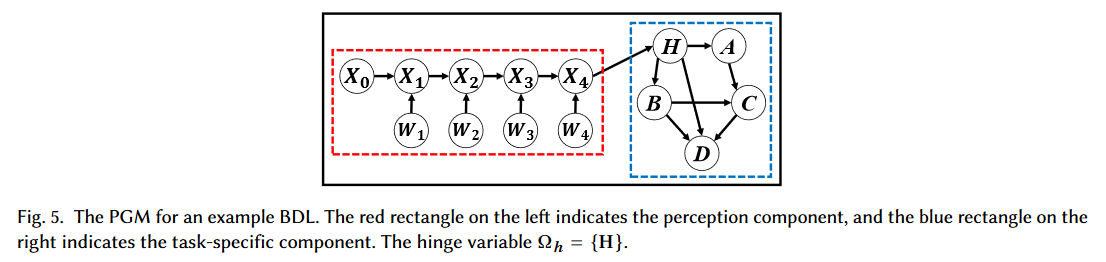
BDL sensu lato refers to the unification of a ‘perception component’, instantiated by a probabilistic neural network, and a ‘task-specific component’, instantiated by a probabilistic graphical model (PGM), under a principled probabilistic framework. Such a unified framework (as shown in the figure below) therefore enables end-to-end learning and inference. Here the ‘perception component’ can be the Bayesian version of neural networks, i.e., Bayesian neural networks (BNN) [3], or just some simplified version of BNN.

BDL sensu stricto refers to BNN itself. Therefore BDL sensu strico can be seen as a component, or more specifically the ‘perception component’ of BDL sensu lato. We note that BNN itself is already a decades-old topic. It starts with a classic paper by David MacKay in 1992 [3], probably before PGM was born; naturally this is different from BDL sensu lato where PGM is an indispensable component. Hence in the following, when we mention BDL, we will be referring to BDL sensu lato.

Why BDL

One natural question is: why does BDL need both (deep) neural networks and graphical models? Shouldn’t neural networks suffice? This is because neural networks cannot natively support (1) conditional inference, (2) causal inference, (3) logic deduction, and (4) uncertainty modeling. Note that ‘cannot natively support’ doesn’t mean ‘cannot support’. Ultimately a neural network is just a (differentiable) function, therefore one may be able to borrow some ideas from PGM, design a ‘sophisticated’ neural network to enable a subset of the four functionalities mentioned above, and say ‘Look! Neural networks can support X and Y’. However, under the hood it is still the theory of PGM (and possibly others) that is in play. In contrast, BDL tries to provide a unified deep learning framework that natively supports all four functionalities mentioned above.

An Example

From CDL to BDL: Back in 2014, we developed a model called Collaborative Deep Learning (CDL) [2] that significantly improves recommender systems’ performance and receives a lot of attention. Here CDL can actually be seen as a concrete example of applying the BDL framework to recommender systems. In CDL, the ‘perception component’ efficiently processes high-dimensional data (e.g., text or images), while the ‘task-specific component’ incorporates the conditional dependencies among users, products, and ratings via PGM (see the figure below).

After the proposal of CDL, in 2015 we generalized it to a BDL framework (BDL sensu lato mentioned above) [9]. In the past six years a myriad of models across various domains are proposed under this BDL framework. See the table below.

Key Concepts in BDL

One framework, two components, and three variable sets: The key to BDL is what we called ‘One framework, two components, and three variable sets’. In the survey paper, we summarize various mathematical tools that can be used as instantiations of BDL’s ‘perception components’ and ‘task-specific components’:

1. ‘Perception components’ can be instantiated using various probabilistic neural networks such as Restricted Boltzmann Machine (RBM), Probabilistic Autoencoder [2], VAE [4], and Natural-Parameter Network [5].

2. ‘Task-specific components’ can be instantiated using traditional (static) Bayesian networks, deep Bayesian networks [6], or even stochastic processes [7]. Interestingly, stochastic processes can actually be viewed as a type of dynamic Bayesian networks [8]. Note that traditional Bayesian networks are usually static and ‘shallow’.

As for the ‘three variable sets’:

1. ‘Perception variables’ refer to variables inside the ‘perception component’ (see the variables in the red box of Fig. 5 above). These variables are usually drawn from relatively simple distributions (e.g., Dirac delta distributions or Gaussian distributions), and the graph among them is usually simple as well. This is to ensure low computational complexity; otherwise multiple layers of ‘perception variables’ will be computationally prohibitive. This is actually the reason why we need probabilistic neural networks here, since they can be efficiently learned via backprop (BP).

2. ‘Hinge variables’ refer to variables inside the ‘task-specific component’ with direct connections to the ‘perception component’ (e.g., variable H in Fig. 5 above). Their job is to connect these two components and facilitate bidirectional, fast communication between them.

3. ‘Task variables’ refer to variables inside the ‘task-specific component’ without direct connections to the ‘perception component’ (e.g., variable A to D in Fig. 5 above). In contrast to ‘perception variables’, ‘task variables’ can be drawn from various complex distributions and the graph connecting them can be more complicated. This is to better describe the complex conditional dependencies among the task variables.

Above is the overall framework of BDL. We can see that this is quite a general framework with broad potential applications. Even Bayesian neural networks can be seen as a BDL model without any task-specific components. Besides the general framework, we also provide several concrete examples on how one can apply BDL to (1) supervised learning (with recommender systems as an illustrating application), (2) unsupervised learning (with topic models as an illustrating application), and (3) general representation learning (with control as an illustrating application). Table 1 summarizes BDL models developed over the years across various domains. For a more detailed and updating list, I highly recommend you take a look at our Github page.

Last but not least, we try to keep the survey as comprehensive as possible. If you spot any missing references, feel free to contact us: )

References

[1] A survey on Bayesian deep learning. Hao Wang, Dit-Yan Yeung. ACM Computing Surveys (CSUR), to appear, 2020.

[2] Collaborative deep learning for recommender systems. Hao Wang, Naiyan Wang, Dit-Yan Yeung. KDD, 2015.

[3] David MacKay. A practical Bayesian framework for backprop networks. Neural computation, 1992.

[4] Auto-encoding variational Bayes. Diederik P. Kingma, Max Welling, ArXiv, 2014.

[5] Natural parameter networks: A class of probabilistic neural networks. Hao Wang, Xingjian Shi, Dit-Yan Yeung. NIPS, 2016.

[6] Bidirectional inference networks: A class of deep Bayesian networks for health profiling. Hao Wang, Chengzhi Mao, Hao He, Mingmin Zhao, Tommi S. Jaakkola, Dina Katabi. AAAI, 2019.

[7] Deep graph random process for relational-thinking-based speech recognition. Huang Hengguan, Fuzhao Xue, Hao Wang, Ye Wang. ICML, 2020.

[8] Machine learning: A probabilistic perspective. Kevin P Murphy. MIT press, 2012.

[9] Towards Bayesian deep learning: A framework and some existing methods. Hao Wang, Dit-Yan Yeung. TKDE, 2016.